40-32/2 =40-16 =24 =4*3*2*1 =4!deleted by creator
The joke was also explained in the title of the post “A Very Emphatic Answer” which highlights the exclamation mark (emphasis) on the answer as being important.
deleted by creator
I certainly did not get it until you said the thing
I was primed by Reddit to expect the r/unexpectedfactorial
Ah shit. I almost hate this one more than loss.
I hate how these things always come up because “order of operations!” It’s mostly people who are bad at math remembering one topic they struggled with and finally got right, and now they know it’s a touchy subject so it will drive engagement. It’s the modern equivalent of “Mathematicians hate this one secret for solving equations! Click to find out!” Pure engagement bait.
But in all the engineering ive done, things never really come up like this. If there is any potential clarity issues, parentheses would be used, or it would be formatted in a way that makes it much more clear.
40 - (32/2), or 40 - ³²⁄₂ has no clarity issues imo. You don’t even have to think about order of operations because 32 halves is a number on its own. it isn’t an “operation” to do necessarily, it’s a fraction to reduce.
And yes, I get the joke. The joke is making fun of the engagement bait of “some people will get the order of operations wrong!”
The joke
(40 - 32)/2 = 4
If you stop here, you used the wrong order of operations. This is where the the fights normally start in the replies.
but the kid said “4!” not “4”
40 - (32/2) = 24 = 4 * 3 * 2 * 1 = 4!
s. If there is any potential clarity issues, parentheses would be used, or it would be formatted in a way that makes it much more clear.
It reminds me of a very old xkcd that posits "communicating badly and acting smug when you’re misunderstood is not cleverness "
I knew XKCD is based, but this is new level
I mean, xkcd numbers its comics sequentially, and he’s well into the 2000’s now, so a 1xy comic is ancient. Looks like at times, old xkcd was brutal.
Especially hat guy.
Who’s on first? :-)
It’s the same as “only 2% of people get this right! If you get it right you have a very strong brain!”. It’s just a little more devious about it.
Exactly. if only 2% of people get it, perhaps you’re just shitty at communicating.
Love the insight on the bait.
Thanks for the mathsplanation too.
It does leave ambiguity with it being an, apparent, quote/dialogue. Correct and Incorrect are both correct depending on your POV and how you interpret social media posts
Removed by mod
40-32/2 _ 4!
40-16 _ 2×3×4
30-6 _ 2×12
24 = 24
Checks out.
deleted by creator
I’ll take that as a compliment. 💝
Depends if the kid said “four!” or “four factorial”
all maths must be said in a neutral tone lest you imply factorials
Almost as if the joke relies on the fact that in written form those are the same.
That’s how I say factorial though I just yell
So Italians mathematicians put everything in factorial
Throw up some brackets, you rage-baiting motherfucker!
No actually the trick to this one is that Four-Factorial equals 24
So 40 - 16 = 24
Aha! Fair enough.
This one’s perfectly unambiguous without brackets, unlike the 1/2x stuff
1/2x is also unambiguous. 2a=(2xa) by definition. Has done for at least 180 years. Terms
deleted by creator
Even your “BODMAS” isn’t universal, lots of people learn “PEMDAS” or “BEDMAS”
At any level of mathematics after elementary school, you never see terrible expressions like this. Well, except for facebook and twitter
Take for example: 2/2*2 It is 0.5 or 2 depending on order. But if I were anything after high school (I was more complacent in high school, I guess) if someone gave me an arbitrarily solved equation or expression like this, I would be livid and raise hell at them for trying to do that.
deleted by creator
Yes, the fundamentals the same, higher orders come first. BUT…
-Multiplication comes before division in some forms, like PEMDAS. In the example I use, this changes the answer.
-When you apply an operation, you should specify what it is operating on. In all of these acronyms, addition comes before subtraction, but with a different example:
2 - 2 + 2
The minus sign only applies to the middle term, by convention. It is the equivalent of “adding negative two”. You can quickly see that this expression is equal to 2.
But if you use one of these acronyms, you end with this expression evaluating to -2. I would say it is almost universally accepted that 2 is the correct answer, and -2 is incorrect. Basically, all these acronyms end up being useless waste of time.
I don’t know if I conveyed this the first time, but, as a lover of pure mathematics, this is something that does not have application in life or in study. It’s an utterly useless waste of time. There is never a case where someone give you numbers like this, where it is not clear what order the numbers should be applied in.
Multiplication comes before division in some forms, like PEMDAS. In the example I use, this changes the answer
If you have both multiplication and division then you do them left to right. PEMDAS doesn’t mean multiplication first, nor does BEDMAS mean division first. It’s PE(MD)(AS) and BE(DM)(AS) where the bracketed parts are done left to right.
you should specify what it is operating on
Left associativity means it always operates on the following term. i.e. terms are associated with the sign on their left.
The minus sign only applies to the middle term, by convention
By the rule of left associativity.
But if you use one of these acronyms, you end with this expression evaluating to -2
No it doesn’t. How on Earth did you manage to get -2?
all these acronyms end up being useless waste of time
No they’re not, but I don’t know yet where you’re going wrong with them without seeing your working out.
If you have both multiplication and division then you do them left to right. PEMDAS doesn’t mean multiplication first, nor does BEDMAS mean division first. It’s PE(MD)(AS) and BE(DM)(AS) where the bracketed parts are done left to right.
You are adding more rules to protect a convention that doesn’t work and doesn’t mention them to begin with. If all that matters is higher orders first, then why bother having an acronym? Just say “Brackets, then higher orders”. Bam. Solved it with less words than any of the acronyms.
Left associativity means it always operates on the following term. i.e. terms are associated with the sign on their left.
As someone who studied mathematics, computer science, and engineering in university, I certainly don’t you to tell me how to do bare bones arithmetic. I know operators apply to the numbers to their right. Everyone does. You jumped right on by the point.
With 2/2*2, you don’t know if it is 2*2/2, or 2/(2*2). When you are dividing by numbers, you put them all in the denominator. If I had to put it in a line, I would at least do 2/(2)*2, to show what is in the denominator. If it is ambiguous, you have done it incorrectly.
By the rule of left associativity.
BY CONVENTION, as I said. You don’t have to repeat what I said a second time.
No it doesn’t. How on Earth did you manage to get -2?
wow. geez. I wonder.
If you can’t follow the steps guided for such a simple example, maybe we just shouldn’t have this conversation. It’s not like you could have tried in your head different orders to combine 3 numbers.
You are adding more rules
I’m stating the existing rules.
If all that matters is higher orders first
I don’t even know what you mean by that. We have the acronyms as a reminder of the rules, as I already said.
I know operators apply to the numbers to their right.
If you know that then how did you get 2-2+2=-2?
With 2/22, you don’t know if it is 22/2, or 2/(2*2)
Yes you do - left associativity. i.e. there’s no brackets.
When you are dividing by numbers, you put them all in the denominator
Only the first term following a division goes in the denominator - left associativity.
BY CONVENTION, as I said. You don’t have to repeat what I said a second time.
I didn’t. You said it was a convention, and I corrected you that it’s a rule.
It’s not like you could have tried in your head different orders to combine 3 numbers.
addition first
2-2+2=4-2=2
subtraction first
2-2+2=-2+2+2=-2+4=2
left to right
2-2+2=0+2=2
3 different orders, all the same answer
Even your “BODMAS” isn’t universal, lots of people learn “PEMDAS” or “BEDMAS”
The rules are universal, only the mnemonics used to remember the rules are different
except for facebook and twitter
… and high school Maths textbooks, and order of operations worksheet generators, and…
2/2*2 It is 0.5 or 2 depending on order.
It’s always 2. #MathsIsNeverAmbiguous
The rules are universal, only the mnemonics used to remember the rules are different
The rules and the acronyms describe different things. If you have to make more rules to say M and D are the same, and that you go left to right when you do them, then the basic rules you followed were flawed. The universal conventions of mathematics don’t need these acronyms confusing people.
high school Maths textbooks
I haven’t seen anything since early elementary school, not middle school, and certainly not high school. Regardless, if a textbook has it, it doesn’t make it right at all. If the acronyms are useless to learn, having them in a textbook doesn’t validate them.
and order of operations worksheet generators
…that’s one of the two examples you used? Did you think about that before you typed it out?
It’s always 2. #MathsIsNeverAmbiguous
IT IS AMBIGUOUS IN THIS POST AND ALL EXAMPLES I HAVE SHOWN. That is the problem at hand.
There is no real problem solving in trying to decipher poorly written shit. It’s the equivalent if English classes took time out to give students worksheets with “foder” written on them, and expecting students to find out if the writer meant “folder” or “fodder”- no sentence context, just following a list of “rules”. It is not difficult to write mathematical expressions with clear context to how numbers relate, even with the lazy shortcuts and shorthand that mathematicians love.
The rules and the acronyms describe different things.
No, they don’t.
If you have to make more rules to say M and D are the same,
I didn’t make more rules - that’s the existing rules. Here’s one of many graphics on the topic which are easy to find on the internet…
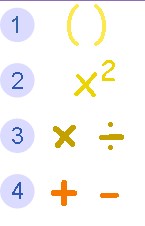
…that’s one of the two examples you used?
Yes. Did you try looking for one and ramping it up to the most difficult level? I’m guessing not.
IT IS AMBIGUOUS IN THIS POST
No, it isn’t. Division before subtraction, always.
ALL EXAMPLES I HAVE SHOWN
None of those have been ambiguous either, as I have pointed out.
That is the problem at hand.
The problem is people not obeying the rules of Maths.
There is no real problem solving in trying to decipher poorly written shit
It’s not poorly written. It’s written the exact way you’d find it in any Maths textbook.
It’s perfectly reasonable to read this as both (40-32)/2 and 40-(32/2) anywhere past basic math.
No, it isn’t. Division before subtraction.
And that kids name? Mathew Matician.
The kid who got it wrong? Numbers McCountyFingers.
Intentionally writing equations shittily is a special type of brain rot.
40 - (32 / 2) = ?
Ftfy.
The cleverness is that it works either way
40-16=4!
8/2=4
But then there’s no joke/trick.
deleted by creator
It really is.
Just because it can be written The original way doesn’t mean it should be. It’s like developers that use obscure or single letter variables instead of descriptive variables. Sure, you can write variables in an obtuse manner, but it’s better for everyone if you write them in a descriptive manner.
fun fact, ? = sqrt(-|x| / 0) for all real x
Nothing wrong with the way it’s written - division before subtraction.
I actually remember seeing this on my YouTube feed. I was pretty confused at first until I saw the factorial sign.
OH!
Where is the bell curve
Not related. I love your username

Reject tradition, embrace crab
it’s wrong, because:
- i would never ask a kid something like that
- there is a question mark missing
- i don’t know any kids and they would probably just flip me off in that situation, which is okay, because they shouldn’t talk to strangers
Such a great post lmao
What enrages me is the pairing of “wrong” and “correct”.
With pemdas correct if written, incorrect if spoken. Ignoring pemdas the opposite. And verbally if the exclamation is not spoken as factorial
4 factorial is correct lol
Yee, I was in the midst of correcting myself since I was typing off my memory
deleted by creator


















